NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers
NCERT Solutions for Class 10 Maths Chapter 1: The entire chapter deals with the concepts and theorems related to Real Numbers, their types, and the operation of real numbers. Euclid's division algorithm and the Unique Prime Factorization Theorem, also known as the Fundamental Theorem of Arithmetic, are the important topics to be considered in this chapter. Euclid's algorithm given in Maths Chapter 1 Real Numbers deals with the divisibility of the integers, and it is used to compute the Highest Common Factor (HCF), whereas the Fundamental Theorem of Arithmetic is used to express the composite numbers as the multiple of prime numbers. They are considered for positive integers only with a condition of divisor not equal to zero.
Euclid's division theorem states that if "a = bq + r", where the range of r lies between 0 and b. When Euclid's division algorithm is applied on given two positive integers, if the remainder (r) is zero, then "b" is the HCF of "a". The Fundamental Theorem of Arithmetic states that every composite number can be written as the product of the powers of primes.
The NCERT Maths Chapter 1 Real Numbers further discusses the concept of rational and irrational numbers. A number is called irrational if it cannot be represented in the form of a/b where a and b both are integers, and b is not equal to zero.
In the case of rational numbers, these are the numbers that can be expressed in the form of a fraction, i.e. in the form of a/b, where both the numerator and denominator are integers, the denominator is not equal to zero. It can have either a terminating decimal expansion or a non-terminating repeating decimal expansion.
Use Euclid’s Division Algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:
Ex 1.1 Class 10 Maths Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution
Ex 1.1 Class 10 Maths Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
Ex 1.1 Class 10 Maths Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution:
Ex 1.1 Class 10 Maths Question 5.
Use Euclid’s Division Lemma to show that the cube of any positive integer is either of the form 9m, 9m + 1 or 9m + 8.
Solution: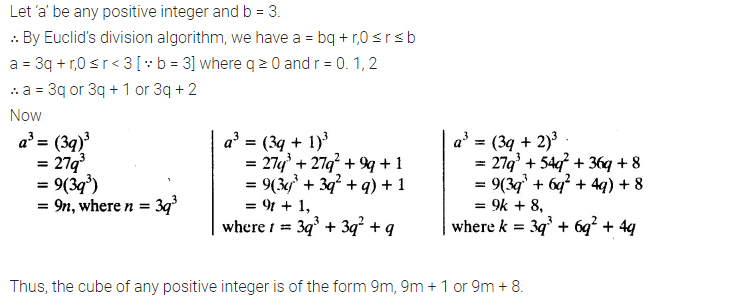
Exercise 1.2
Ex 1.2 Class 10 Maths Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution: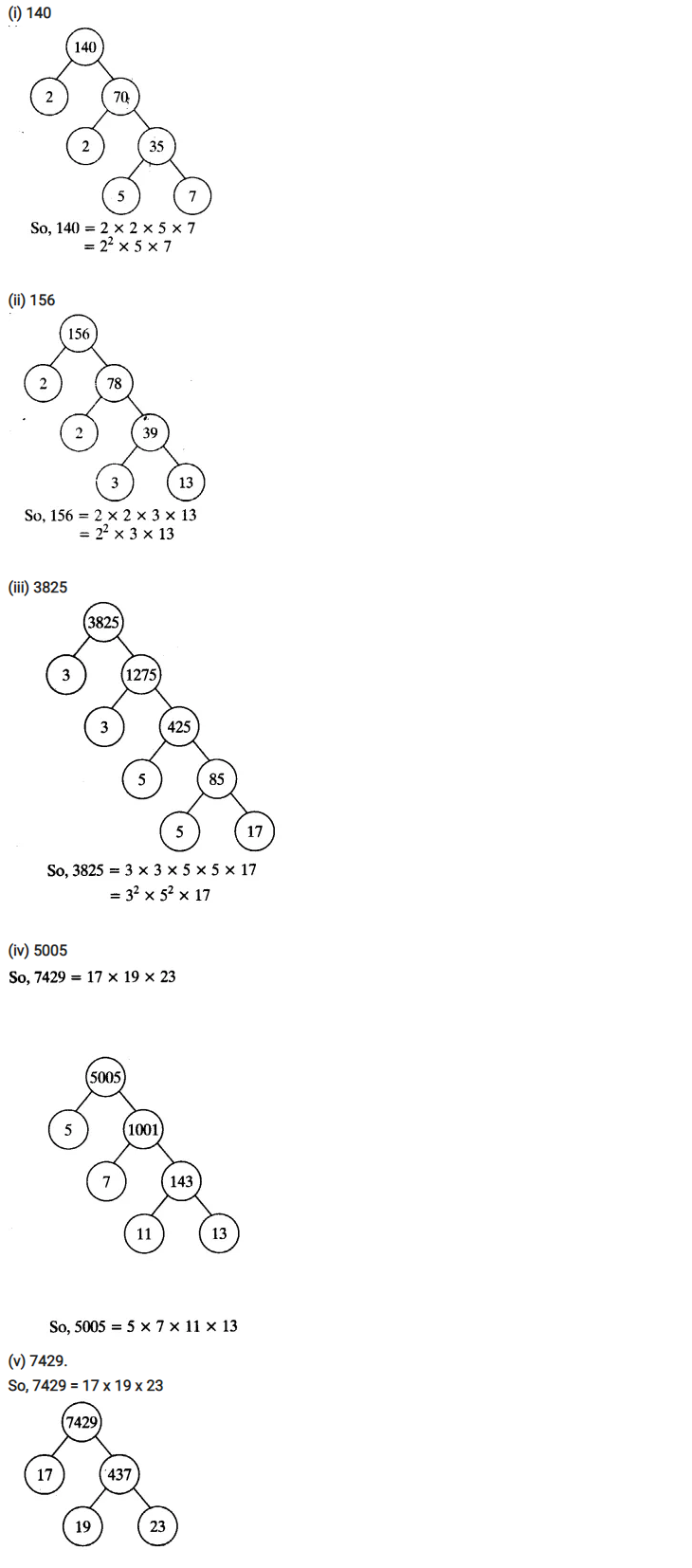
Ex 1.2 Class 10 Maths Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
Ex 1.2 Class 10 Maths Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:
Ex 1.2 Class 10 Maths Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).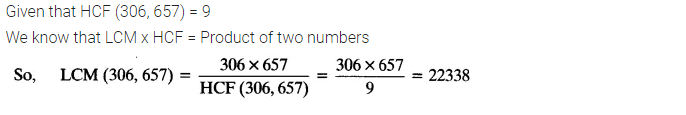
Ex 1.2 Class 10 Maths Question 5.
Check whether 6n can end with the digit 0 for any natural number n.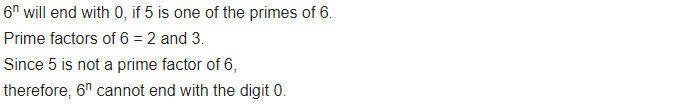
Ex 1.2 Class 10 Maths Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.
Ex 1.2 Class 10 Maths Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Exercise 1.3
Ex 1.3 Class 10 Maths Question 1.
Prove that √5 is irrational.
Solution:
Ex 1.3 Class 10 Maths Question 2.
Show that 3 + √5 is irrational.
Solution:
Ex 1.3 Class 10 Maths Question 3.
Prove that the following are irrational.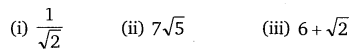
Solution:



